A geometric view of division by a complex number

If you’ve taken a class involving complex numbers, you were likely introduced to the following equality: 

where \(z\) is the complex number \(a + bi\), and \(\bar{z}\) is its conjugate: \(a - bi\).

I’m hoping to provide some intuition about the meaning of this equality and more generally about complex division and the complex conjugate.

If a complex number is thought of as a directed line segment in the Cartesian plane, multiplication is just an operation that scales and rotates it around the origin. Division is defined as multiplication by the inverse \(1/z\), and is thus also just a rotation and scaling. But \(1/z\) is not a very useful value when \(z\) is in the form \(a+bi\) (rather than polar form). Having the sum \(a+bi\) in the denominator is hard to work with.  The following equality solves this issue:

Since \(\vert z \vert^2\) is a single number rather than a sum, the ratio can be changed to a sum of two ratios. Specifically, \(\dfrac{a}{\vert z \vert^2}\) and \(\dfrac{-bi}{\vert z \vert^2}\) . Only one of these ratios has an i, so we are back in the form consisting of a real component and an imaginary component. Well that’s great and all, but \(\dfrac{\bar{z}}{\vert z \vert^2}\) is rather opaque. Is there a geometric representation of what is going on? Why yes, there is!

Assume we know the polar form of \(z\), that is \(z=re^{i\theta}\) . Consider what happens when we multiply some complex number, 1 for instance, by \(z\):

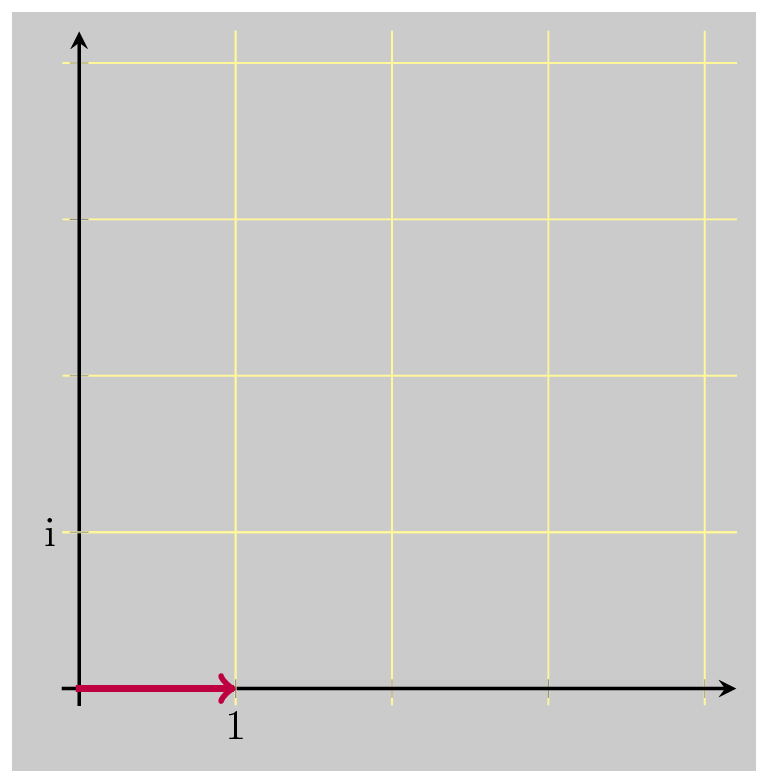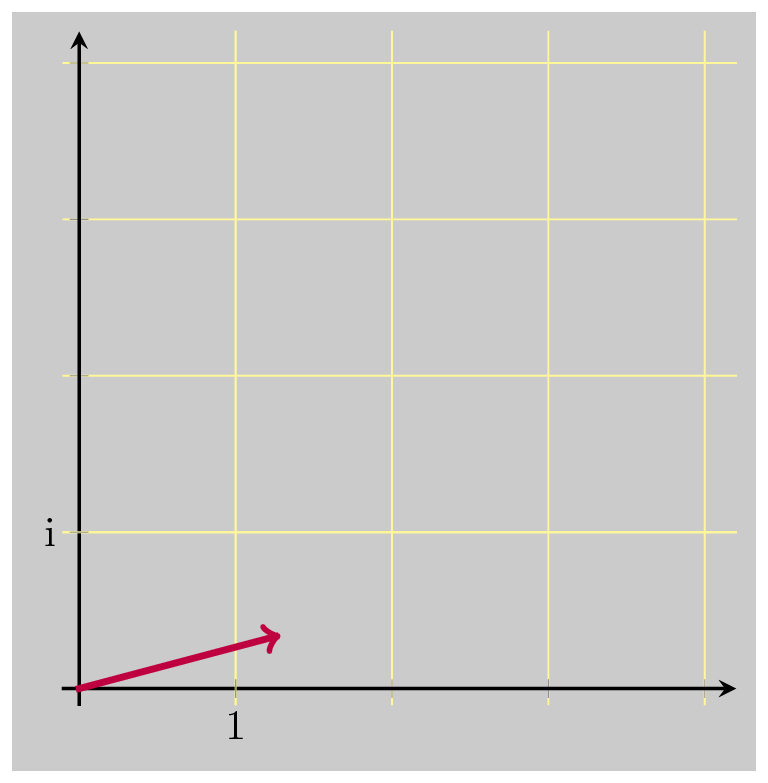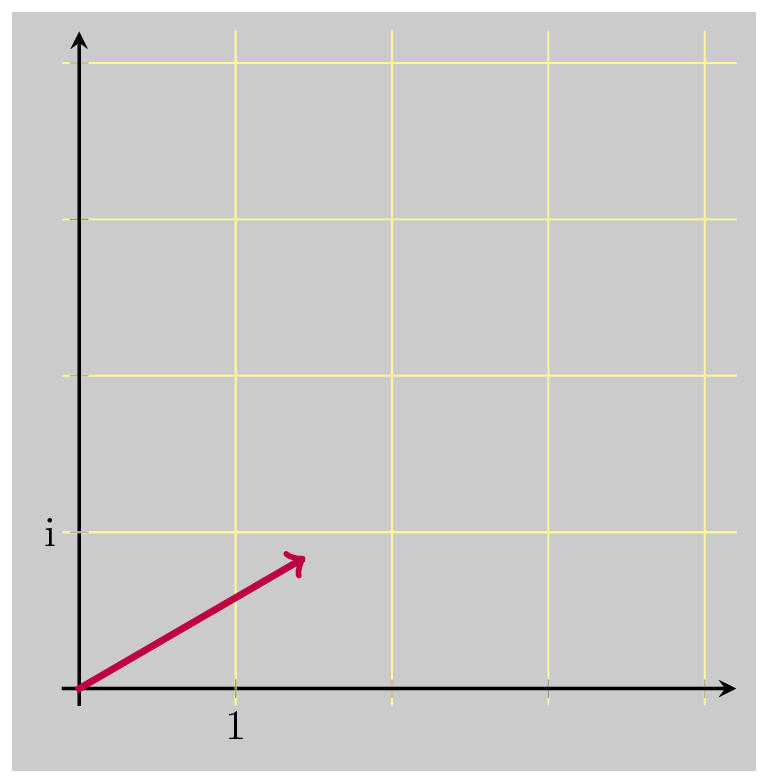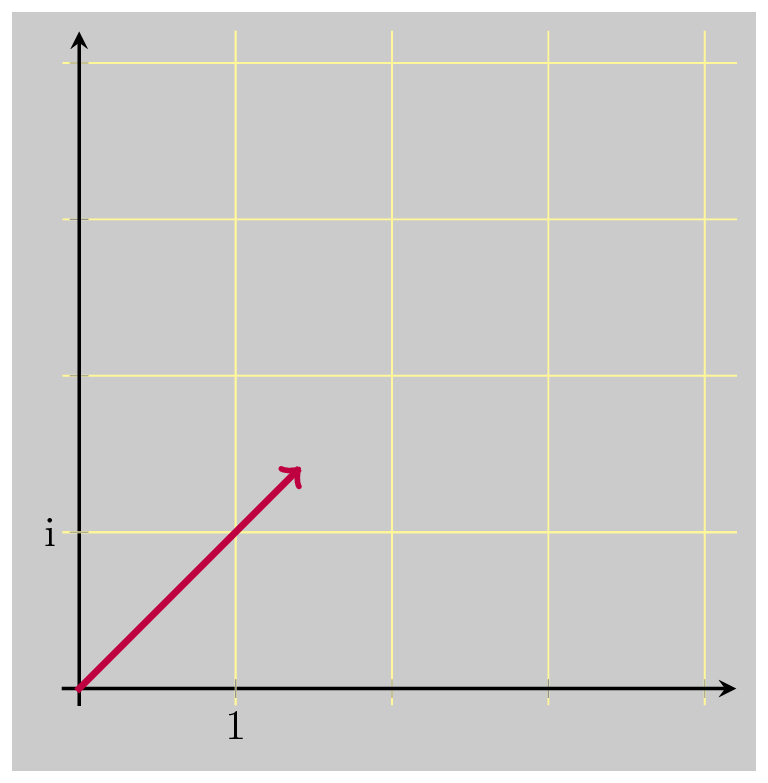
Multiplication by \(z\) simply rotates by \(\theta\) and scales by \(r = \vert z \vert\) . The number that will take us back to 1, reversing the rotation and scaling, is \(\dfrac{1}{z}\) . We know that \(\dfrac{1}{z} = \dfrac{\bar{z}}{\vert z \vert^2}\) , so let’s see what happens when we now multiply by \(\bar{z}\) . Recall that \(\bar{z} = a-bi = re^{-i\theta}\) . So \(\bar{z}\) rotates by an angle of \(-\theta\) . Which is what we want: to undo the original rotation. But multiplying by \(\bar{z}\) does not undo the scaling. In fact, it takes us farther away for the input value 1, scaling up again by \(\vert z \vert\) . This gives us a sense for what the complex conjugate is: a number which rotates in the opposite direction but scales by the same amount.

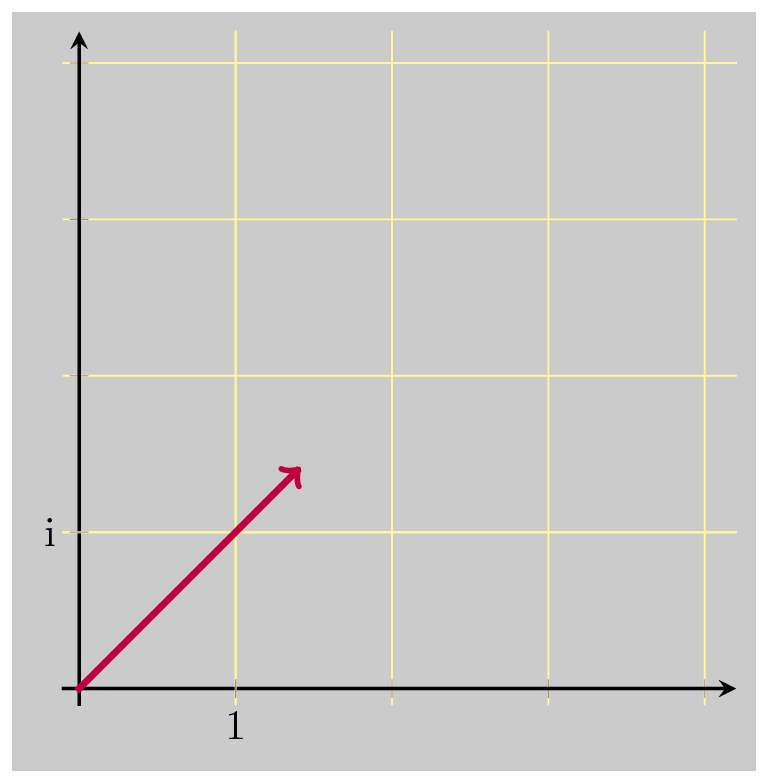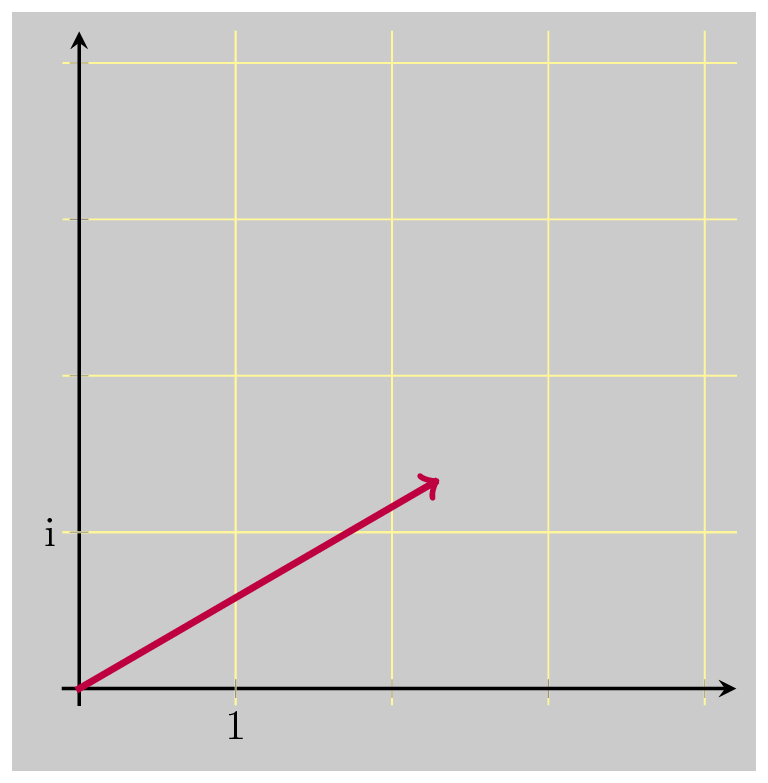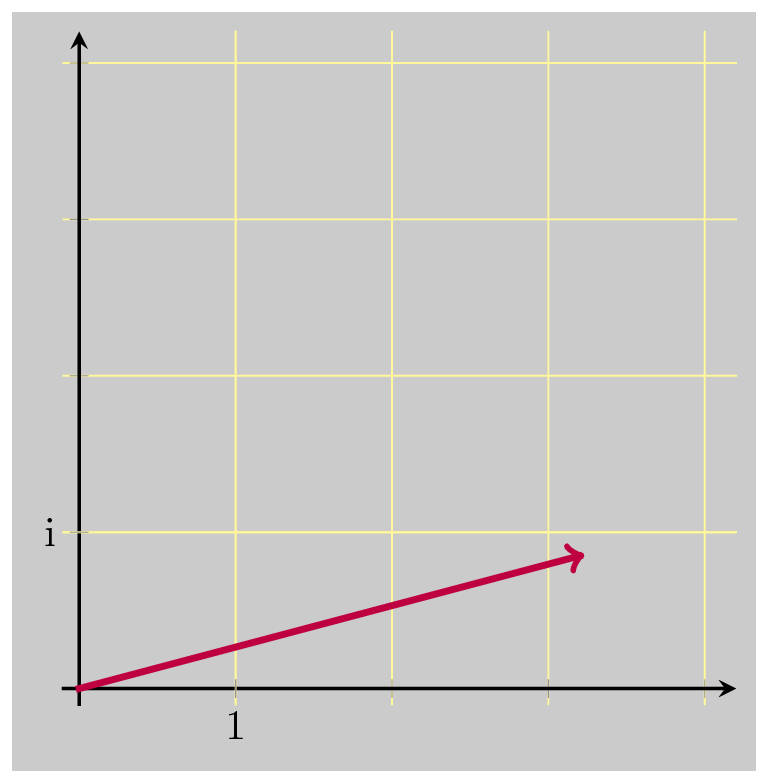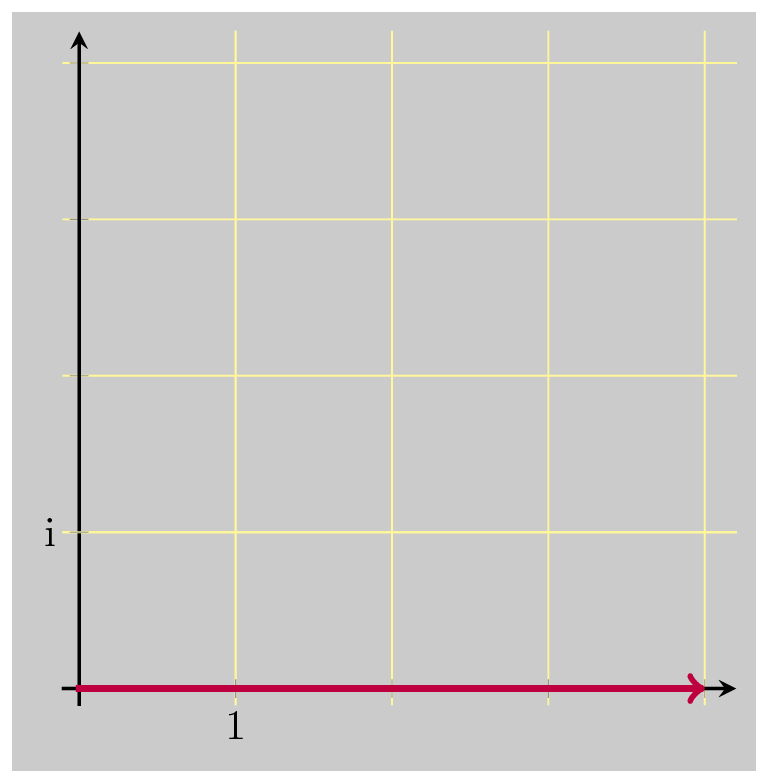
So let’s just scale down that result by \(\vert z \vert\) :

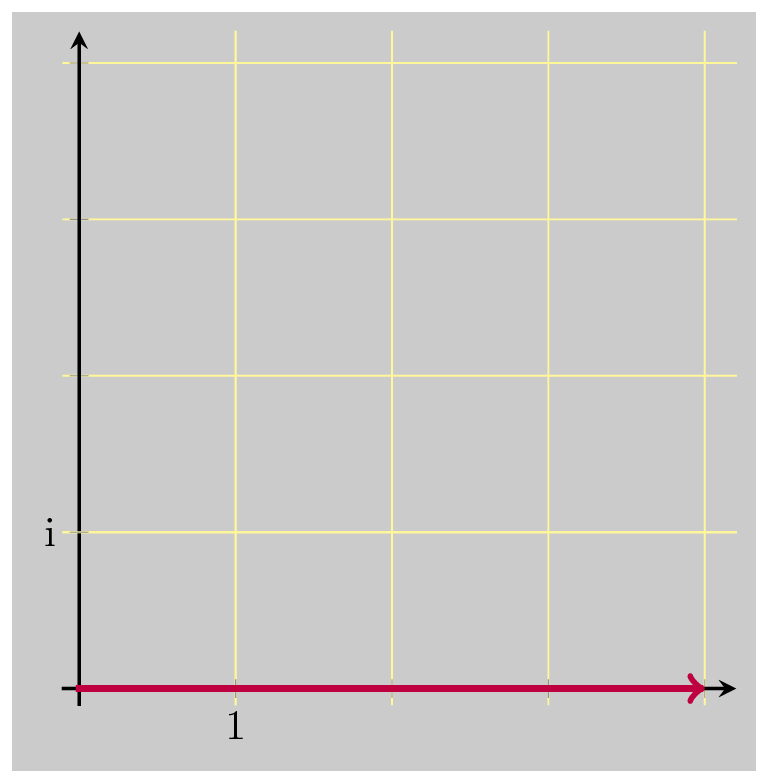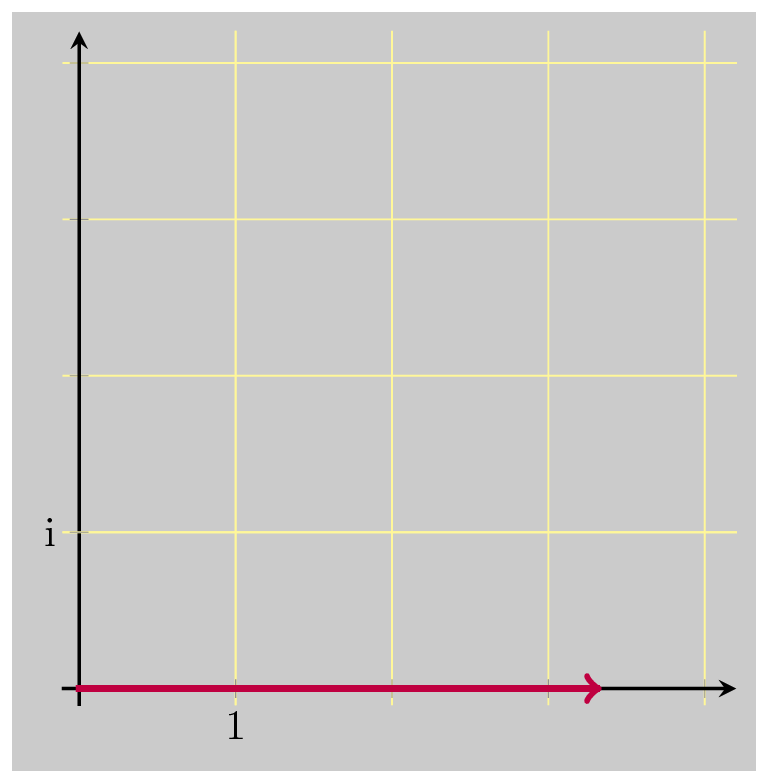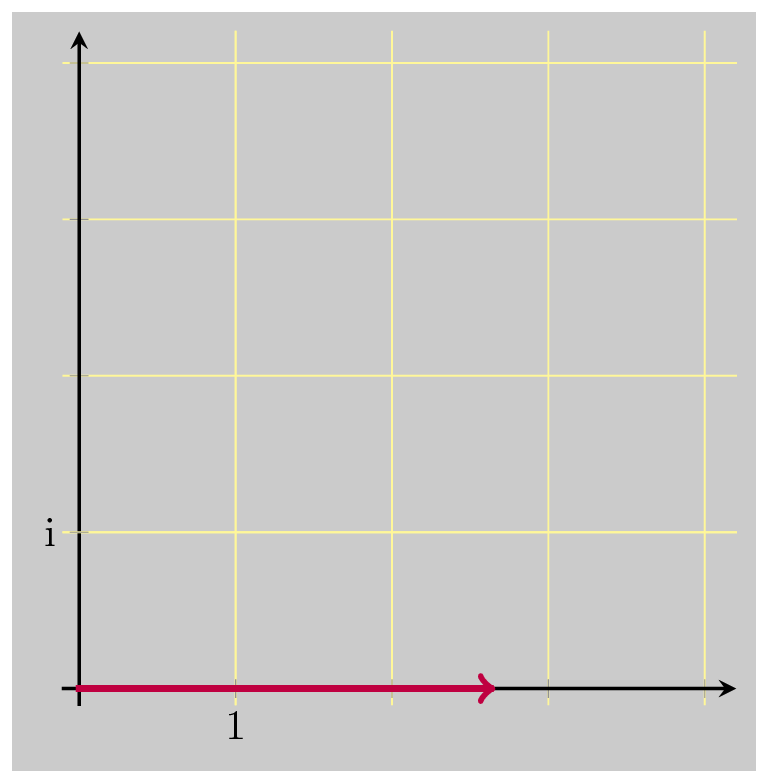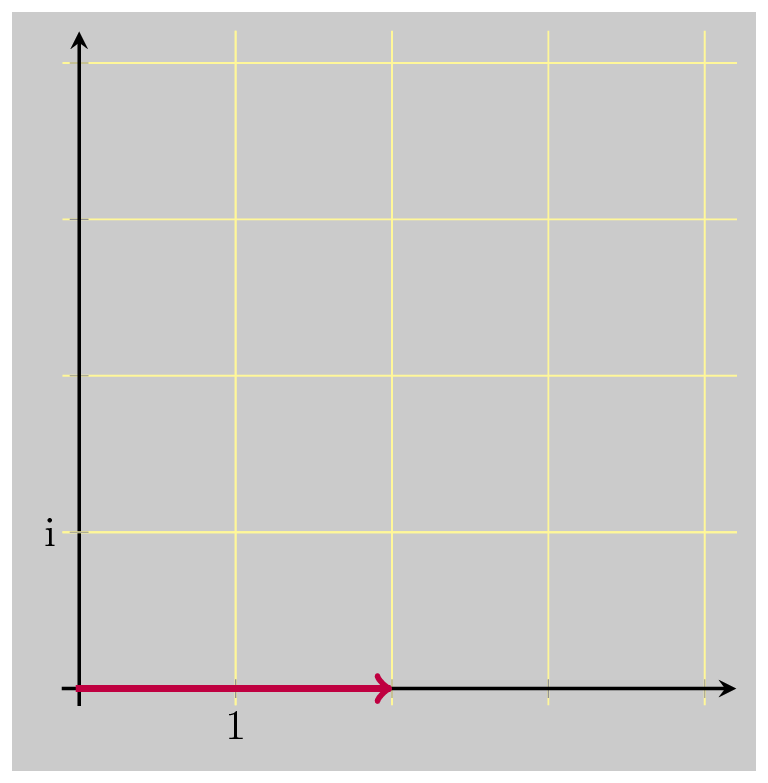
And then scale down just one more time, again by \(\vert z \vert\) :

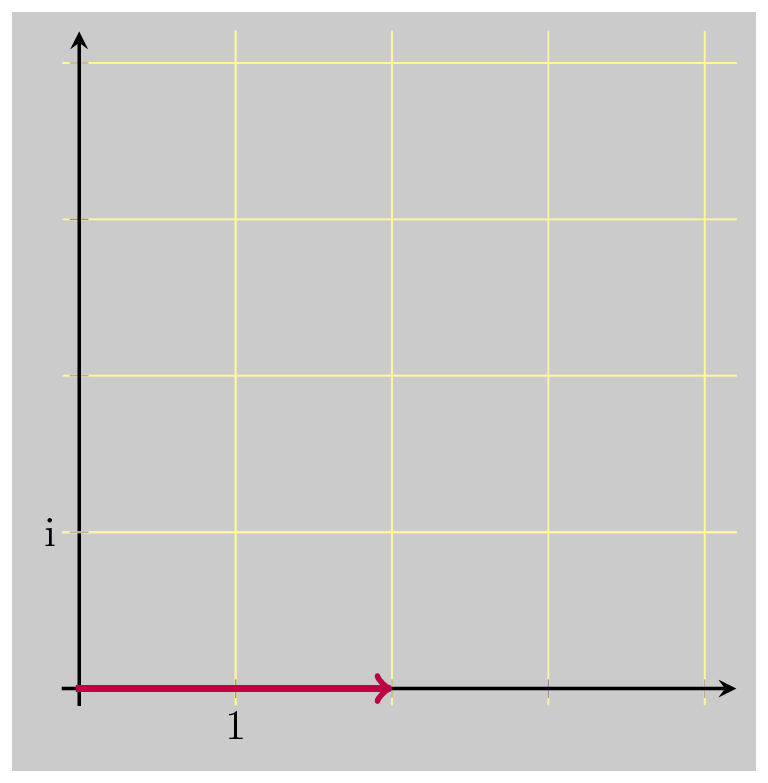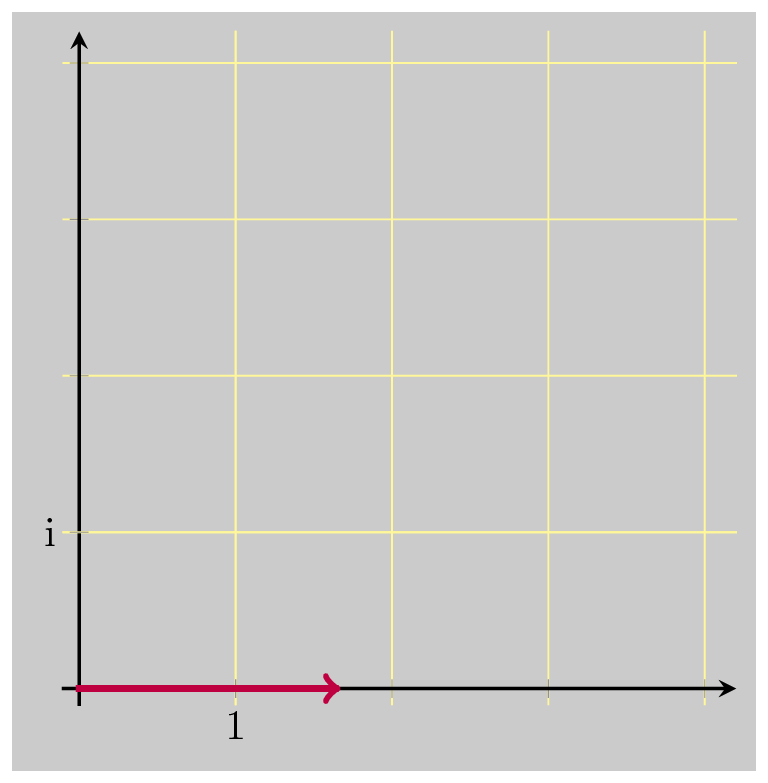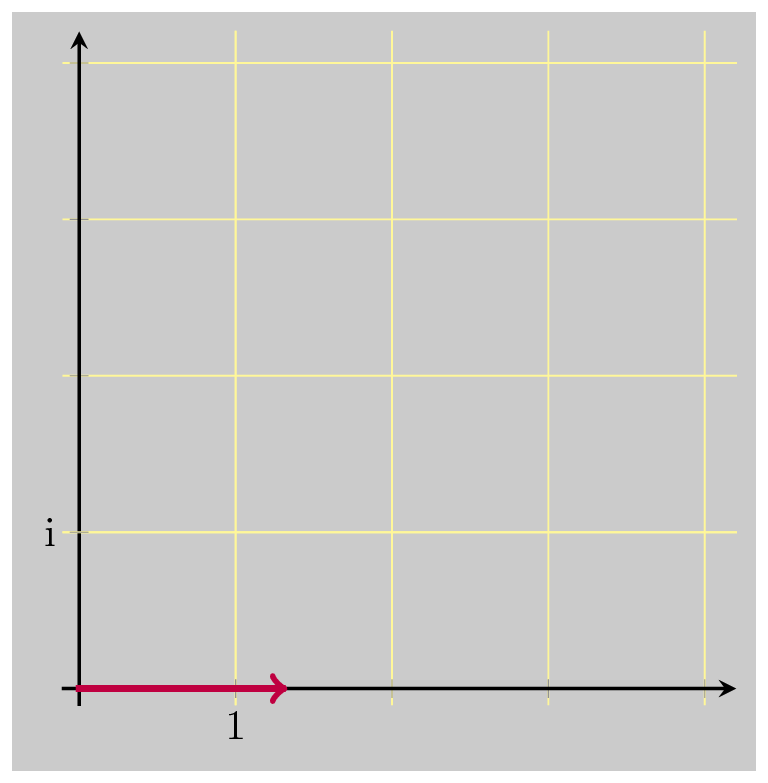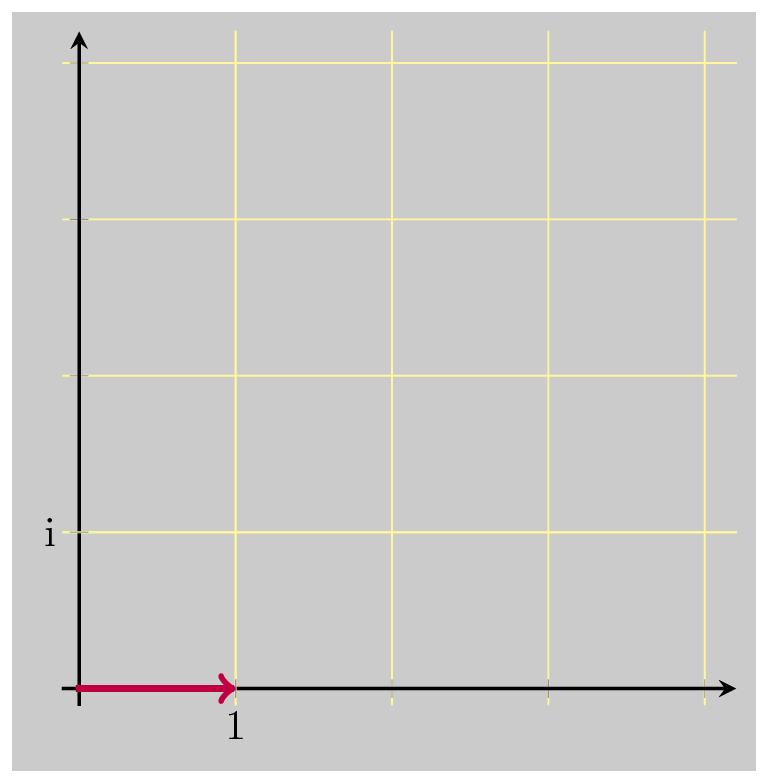
And that did the trick, bringing us back down to 1. So these three operations together are the multiplicative inverse of \(z\) . Multiplying by \(\bar{z}\) undoes the rotation, and scales up by \(\vert z \vert\) . Dividing by \(\vert z \vert\) undoes the scaling that was just added. And dividing by \(\vert z \vert\) again undoes the original scaling when we first multiplied by \(z\) .

And that’s about it folks.

Aside: The plots were done in \(\LaTeX\), you can check out the code on Overleaf. Then a pdf with one page for each frame was exported, and the following bash was run using ImageMagick convert to turn the pdf into a gif:

1
2
3
4
5
6
7
base_name=$1 # base name of pdf to make into gif
pdf="$base_name.pdf"
gif_no_pause="$base_name.no_pause.gif"
gif="$base_name.gif"

convert -dispose background -delay 2 -loop 0 -density 300 $pdf $gif_no_pause
convert $gif_no_pause $$ +clone -set delay 500 $$ +swap +delete $gif

The \(\LaTeX\) is a bit of a mess. This method of plotting and animating was far more time consuming and tedious than it could have been. If you have a suggestion for improving this process, I’d love to hear it.